Двоичная система счисления
Двоичные адреса и адреса IPv4
Адреса IPv4 начинаются как двоичные, последовательность только из 1 и 0. Управлять ими сложно, поэтому сетевые администраторы должны преобразовать их в десятичные. В этом разделе показано несколько способов сделать это.
Двоичная система счисления состоит из цифр 0 и 1, называемых битами. Десятичная система счисления состоит из 10 цифр: от 0 до 9.
Понимание двоичной системы важно для нас, поскольку узлы, серверы и сетевые устройства используют именно двоичную адресацию. В частности, для идентификации друг друга они используют двоичные IPv4-адреса (как показано на рис. 1).
Имеется центральный маршрутизатор с двумя локальными сетями, подключенными напрямую, и одной глобальной сетью, подключенной к облаку. В каждой локальной сети есть коммутатор и ПК. WAN имеет один компьютер. Каждое устройство имеет адрес IPv4, который находится в точечной двоичной записи вместо точечной десятичной записи.
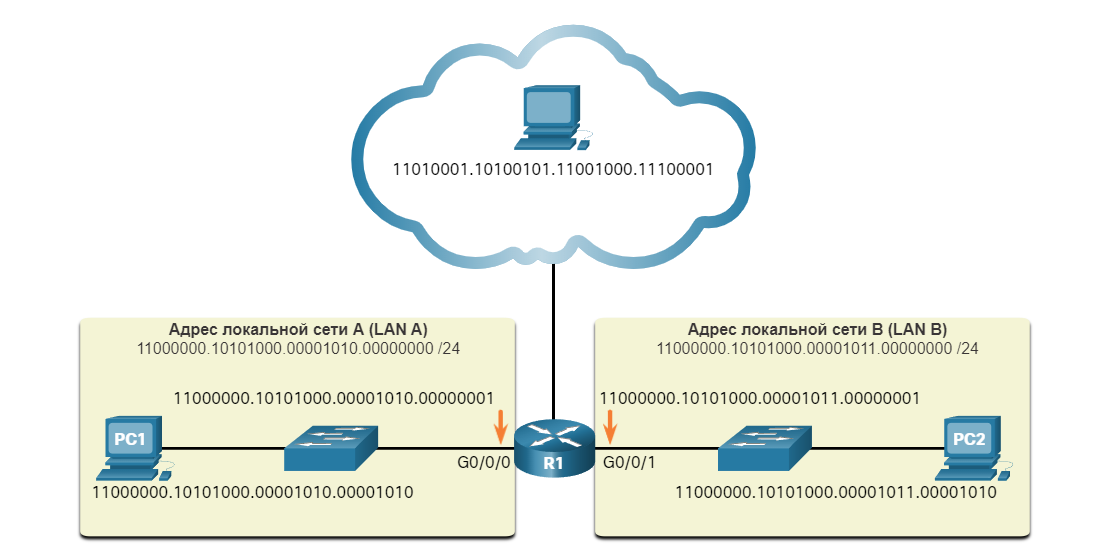
Каждый адрес представляет собой строку из 32 бит, разделенную на 4 части, называемые октетами. Каждый октет содержит 8 бит (или 1 байт), разделенные точкой. Например, узлу PC1 на рисунке назначен IPv4-адрес 11000000.10101000.00001010.00001010. Адресом его шлюза по умолчанию будет соответствующий адрес интерфейса Gigabit Ethernet interface маршрутизатора R1: 11000000.10101000.00001010.00000001.
Двоичный код хорошо работает с хостами и сетевыми устройствами. Однако людям очень сложно работать с ним.
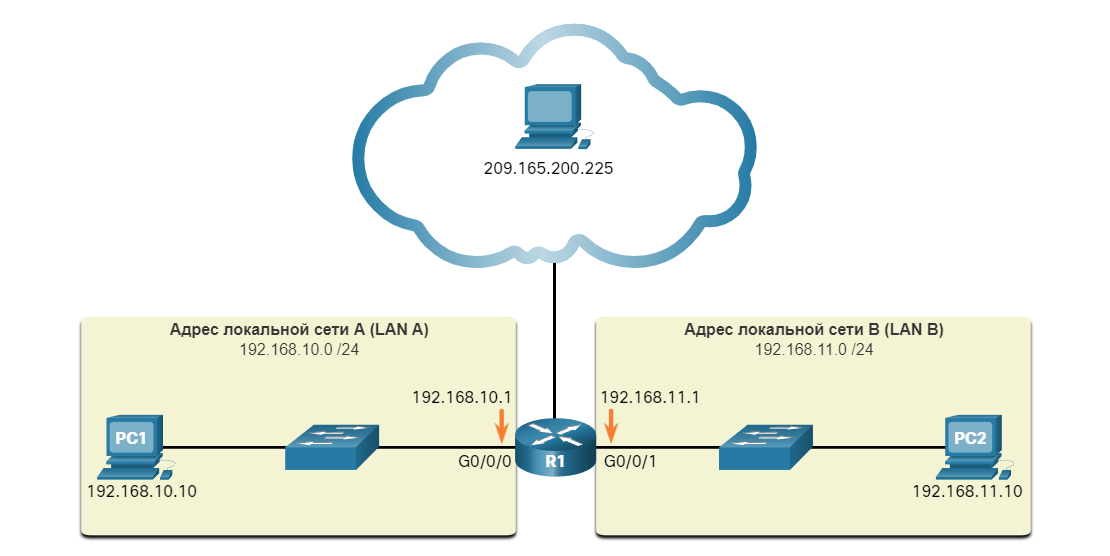
Для простоты использования IPv4-адреса обычно выражаются в десятичном формате с точкой-разделителем. Узлу PC1 назначен IPv4-адрес 192.168.10.10; адрес шлюза по умолчанию — 192.168.10.1, как показано на рисунке.
Эта схема аналогична первому, центральному маршрутизатору с двумя ЛВС и глобальной сетью, подключенной к облаку. Это имеет те же устройства, что и первая диаграмма; однако вместо адресации IPv4 в двоичном виде он находится в точечной десятичной записи.
Для четкого понимания адресации сети необходимо знать принципы двоичной адресации и получить практические навыки преобразования IPv4-адресов из двоичной системы счисления в десятичную с точкой разделителем. В этом разделе вы узнаете, как переводить числа из двоичной в десятичную систему счисления.
Видео. Перевод чисел из двоичной в десятичную систему счисления
Нажмите «Воспроизведение», чтобы увидеть, как двоичный адрес преобразуется в десятичный.
Двоичная позиционная система счисления
Чтобы переводить числа из двоичной в десятичную систему счисления, нужно понимать позиционную систему счисления. Принцип позиционной системы счисления заключается в том, что значение цифры определяется ее «позицией» в последовательности цифр. Вам уже знакома наиболее распространенная система счисления — десятичная (с основанием 10).
В таблице показана суть десятичной системы счисления с точкой-разделителем.
| Основание | 10 | 10 | 10 | 10 |
|---|---|---|---|---|
| Позиция в числе | 3 | 2 | 1 | 0 |
| Вычисление | (103) | (102) | (101) | (100) |
| Позиционное значение | 1000 | 100 | 10 | 1 |
Следующие маркеры описывают каждую строку таблицы.
- Строка 1, Основание - это база числа. Десятичная система счисления имеет основание 10.
2-я строка определяет позицию десятичного числа (справа налево): 0 (1-я позиция), 1 (2-я
позиция), 2 (3-я позиция), 3 (4-я позиция). Эти числа также представляют
экспоненциальное
значение, которое будет использоваться для расчета позиционного значения (4-я строка).
В 3-й строке рассчитывается позиционное значение путем возведения основания в степень,
равную экспоненциальному значению его позиции строки 2.
Примечание: n0 это = 1. - Позиционное значение строки 4 представляет единицы тысячи, сотни, десятки и единицы.
Чтобы воспользоваться позиционной системой, сопоставьте заданное число с его позиционным значением. В примере на рис. 2 показана позиционная запись десятичного числа 1234.
| Тысячи | Сотни | Десятки | Единицы | |
|---|---|---|---|---|
| Позиционное значение | 1000 | 100 | 10 | 1 |
| Десятичное число (1234) | 1 | 2 | 3 | 4 |
| Вычислите | 1 x 1000 | 2 x 100 | 3 x 10 | 4 x 1 |
| Складываем их... | 1000 | + 200 | + 30 | + 4 |
| Результат | 1234 | |||
Напротив, двоичная позиционная запись работает так, как описано в таблице.
| Основание | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
|---|---|---|---|---|---|---|---|---|
| Позиция в числе | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Вычислите | (27) | (26) | (25) | (24) | (23) | (22) | (21) | (20) |
| Позиционное значение | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Следующие маркеры описывают каждую строку таблицы.
- Строка 1, Основание - это база числа. Двоичная система счисления имеет основание 2.
2-я строка определяет позицию двоичного числа (справа налево): 0 (1-я позиция), 1 (2-я
позиция), 2 (3-я позиция), 3 (4-я позиция). Эти числа также представляют
экспоненциальное
значение, которое будет использоваться для расчета позиционного значения (4-я строка).
В 3-й строке рассчитывается позиционное значение путем возведения основания в степень,
равную экспоненциальному значению его позиции строки 2.
Примечание: n0 это = 1. - Позиционное значение строки 4 представляет единицы , двойки, четверки, восьмерки и т.д.
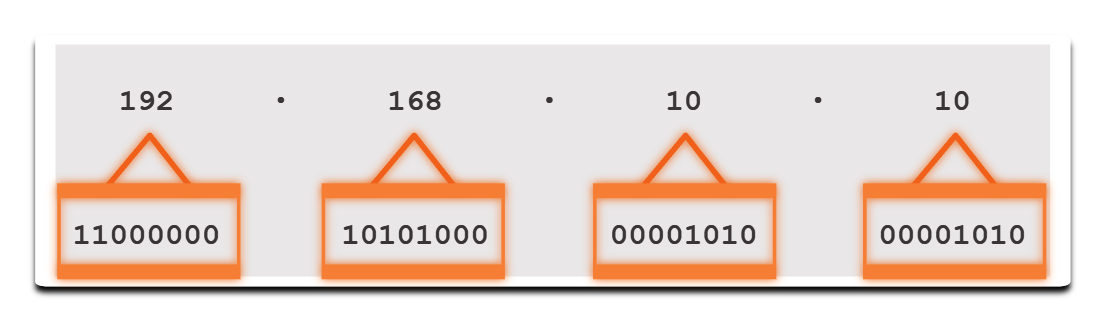
На примере, в таблице, показано соответствие двоичного числа 11000000 десятичному числу 192. Если бы двоичное число составляло 10101000, то ему бы соответствовало десятичное число 168.
| Позиционное значение | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Двоичное число (11000000) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Вычислите | 1 x 128 | 1 x 64 | 0 x 32 | 0 x 16 | 0 x 8 | 0 x 4 | 0 x 2 | 0 x 1 |
| Складываем их .. | 128 | + 64 | + 0 | + 0 | + 0 | + 0 | + 0 | + 0 |
| Результат | 192 | |||||||
Проверьте свое понимание темы - бинарная система чисел
Конвертировать двоичный в десятичные
Для преобразования двоичного IPv4-адреса в десятичный эквивалент с точкой-разделителем, разделите IPv4-адрес на четыре 8-битных октета. Затем занесите двоичное позиционное значение в качестве двоичного числа первого октета и выполните соответствующее вычисление.
Например, предположим, что IPv4-адрес узла — 11000000.10101000.00001011.00001010. Для преобразования двоичного адреса в десятичный формат, начните с первого октета, как показано в таблице. Введите 8-битное двоичное число в качестве позиционного значения строки 1, а затем выполните вычисление, результатом которого будет десятичное число 192. Это число составит первый октет десятичной записи с точкой-разделителем.
| Позиционное значение | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Двоичное число (11000000) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Вычислите | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Складываем | 128 | + 64 | + 0 | + 0 | + 0 | + 0 | + 0 | + 0 |
| Результат | 192 | |||||||
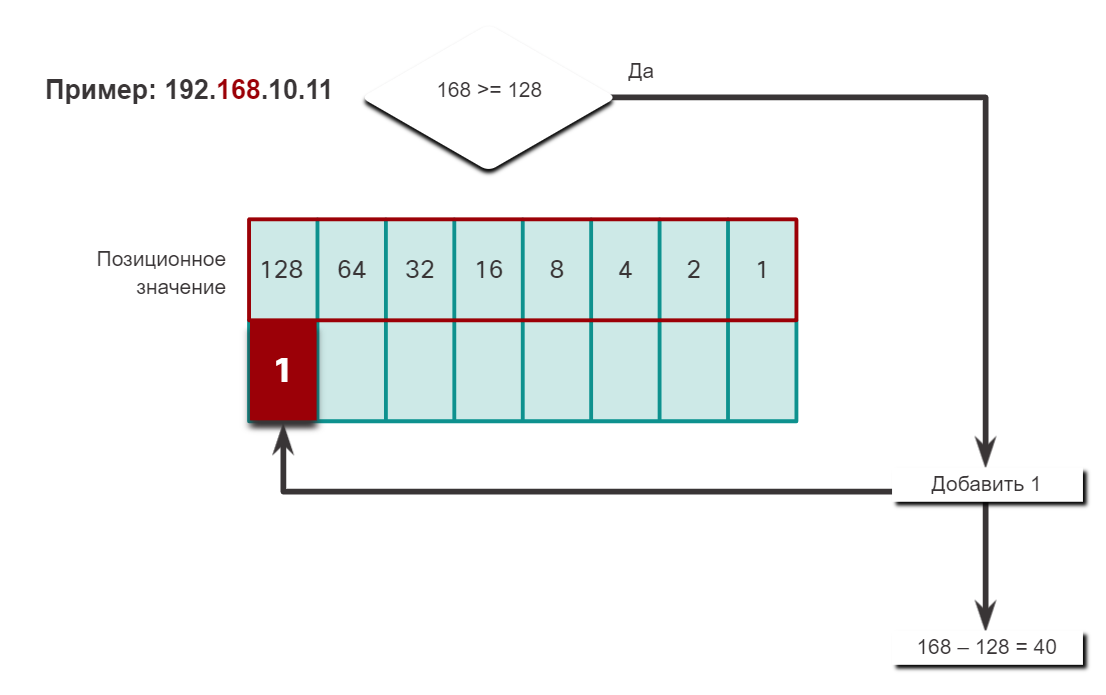
Затем преобразуйте второй октет 10101000, как показано в таблице. Итоговое десятичное значение — 168; это будет второй октет.
| Позиционное значение | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Двоичное число (10101000) | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| Вычислите | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Складываем | 128 | + 0 | + 32 | + 0 | + 8 | + 0 | + 0 | + 0 |
| Результат | 168 | |||||||
Преобразовать третий октет 00001011, как показано в таблице.
| Позиционное значение | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Двоичное число (00001011) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| Вычислите | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Складываем | 0 | + 0 | + 0 | + 0 | + 8 | + 0 | + 2 | + 1 |
| Результат | 11 | |||||||
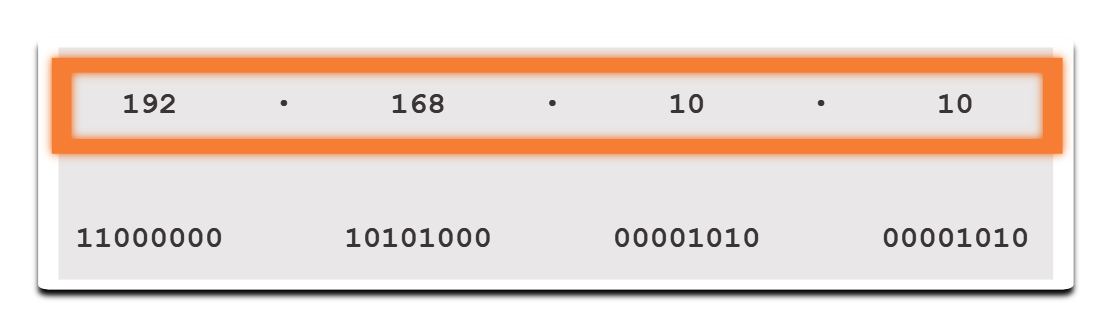
Преобразовать четвертый октет 00001010, как показано в таблице. Это завершает IP-адрес и производит 192.168.11.10.
| Позиционное значение | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Двоичное число (00001010) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Вычислите | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Складываем | 0 | + 0 | + 0 | + 0 | + 8 | + 0 | + 2 | + 0 |
| Результат | 10 | |||||||
Упражнение - преобразование двоичного числа в десятичное
Инструкции
В этом упражнении вы можете на практике отработать преобразование десятичных чисел в 8-битные двоичные значения. Рекомендуется работать с этим инструментом до тех пор, пока вы не сможете выполнить преобразование без ошибок. Конвертировать двоичное число, показанное в октете, до его десятичного значения.
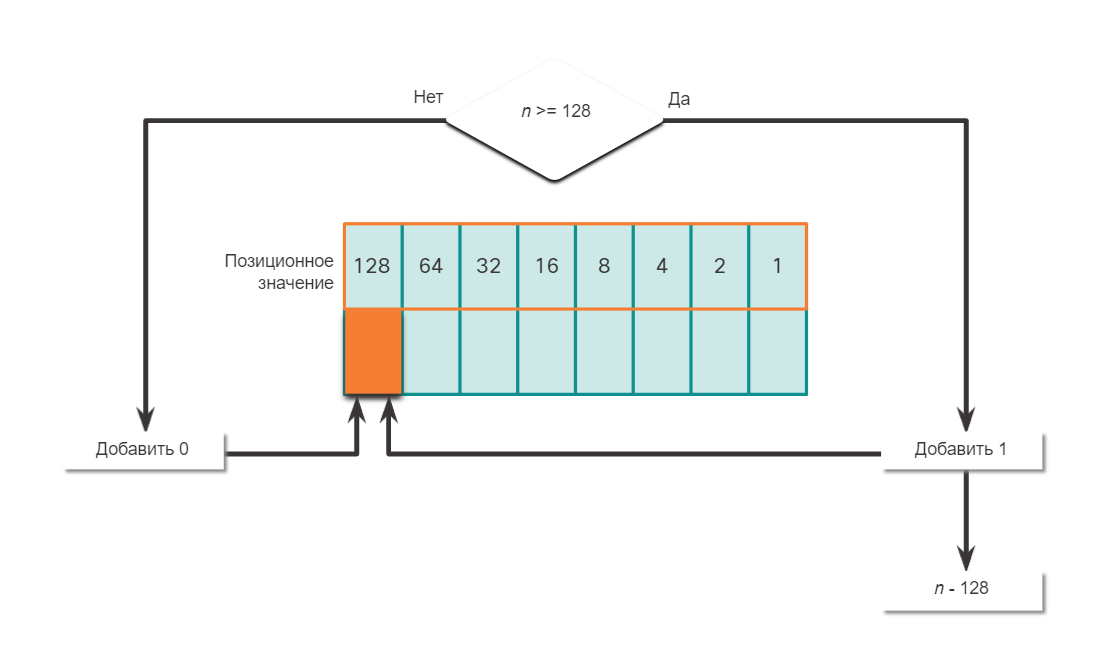
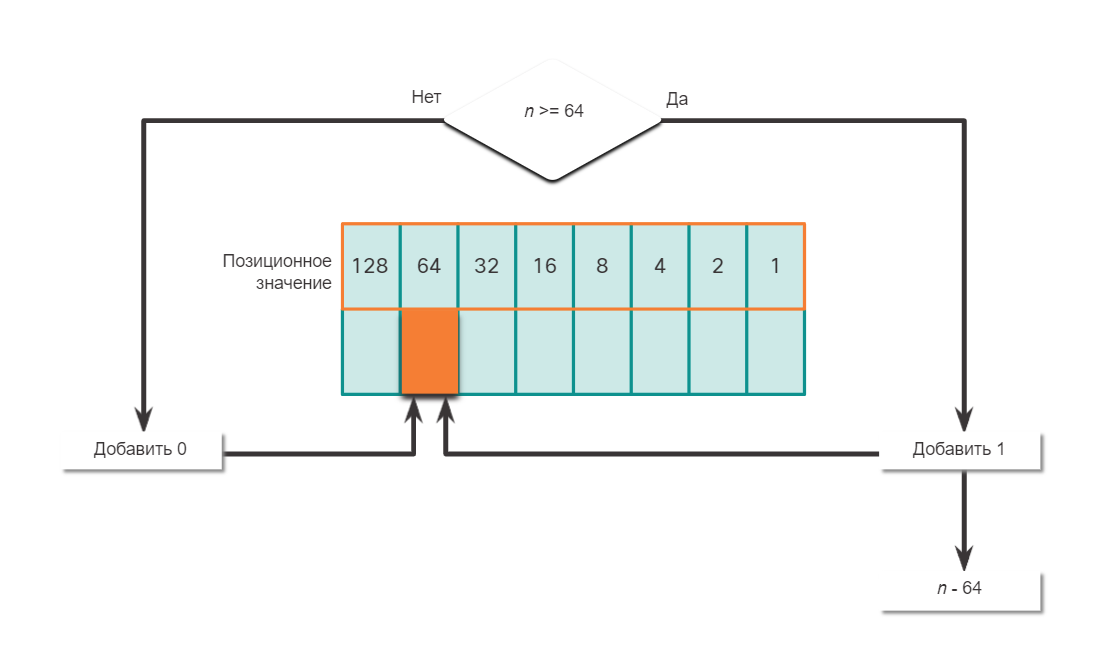
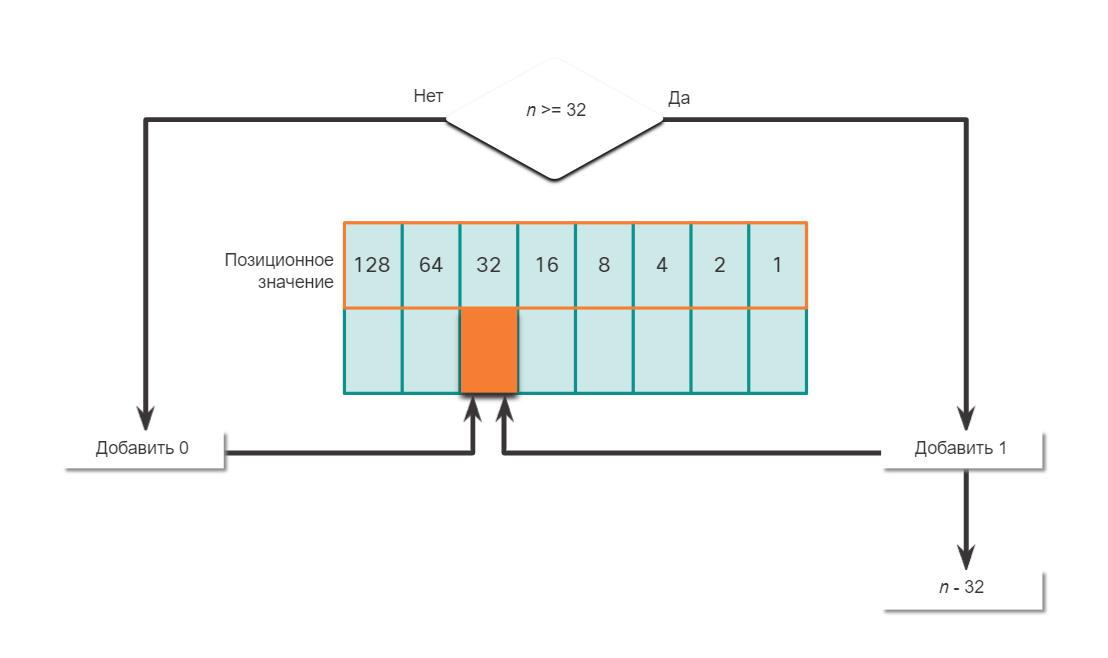
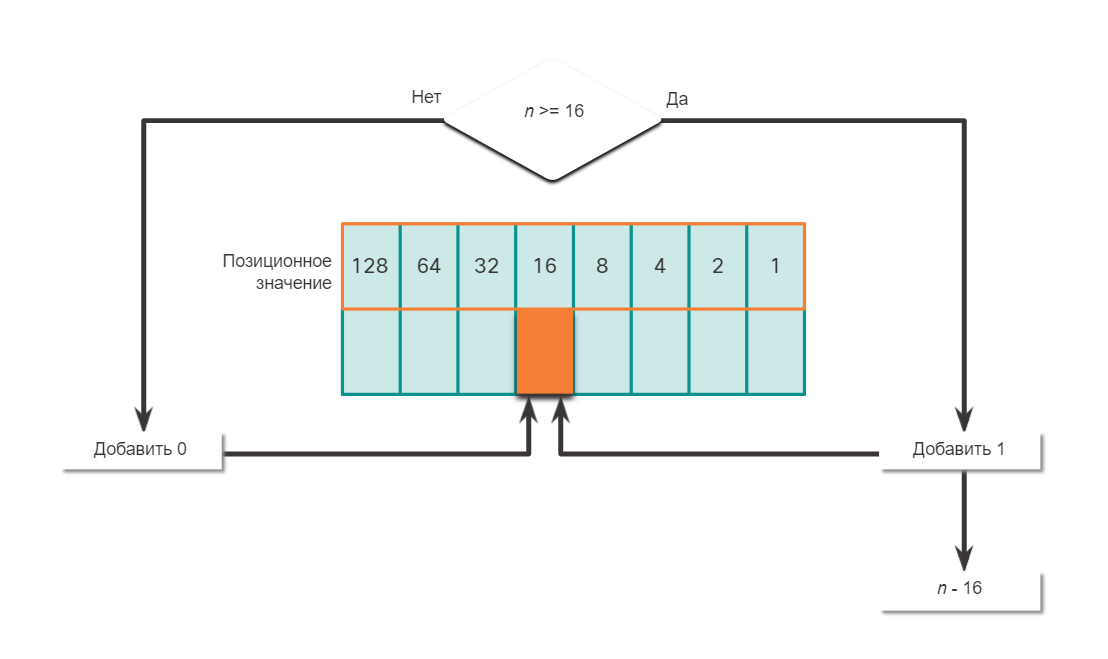
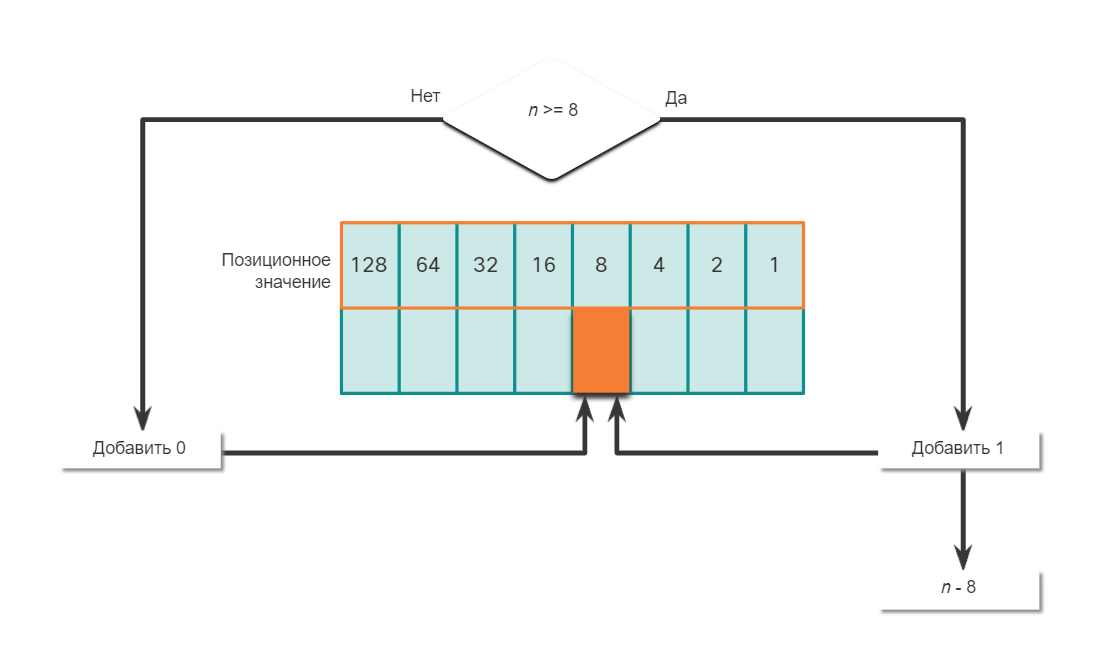
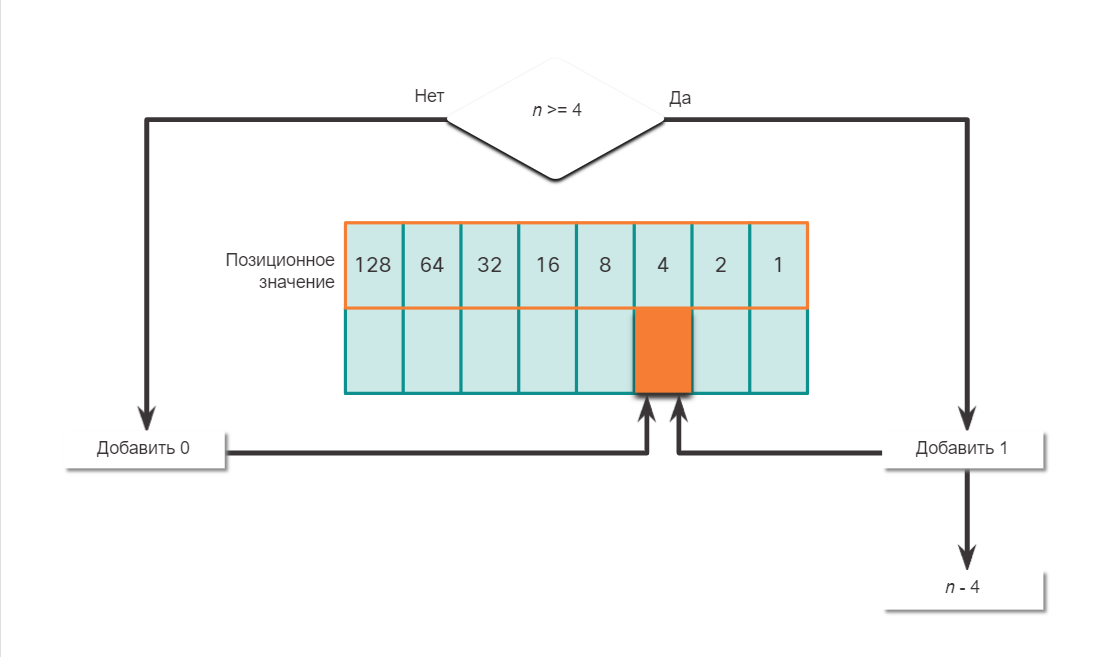
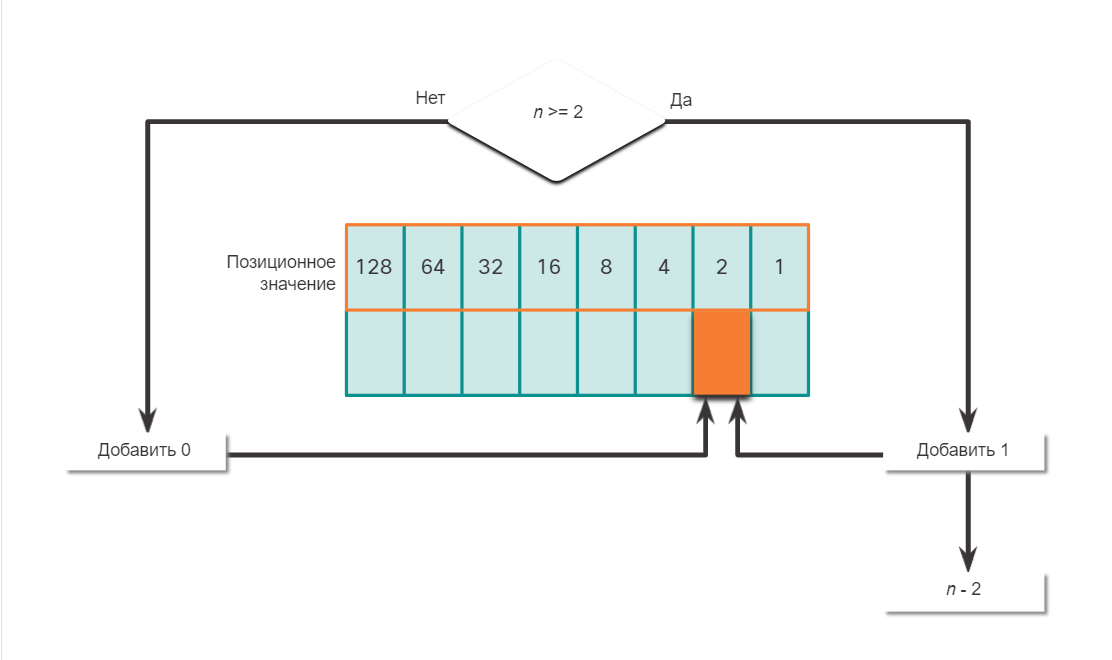
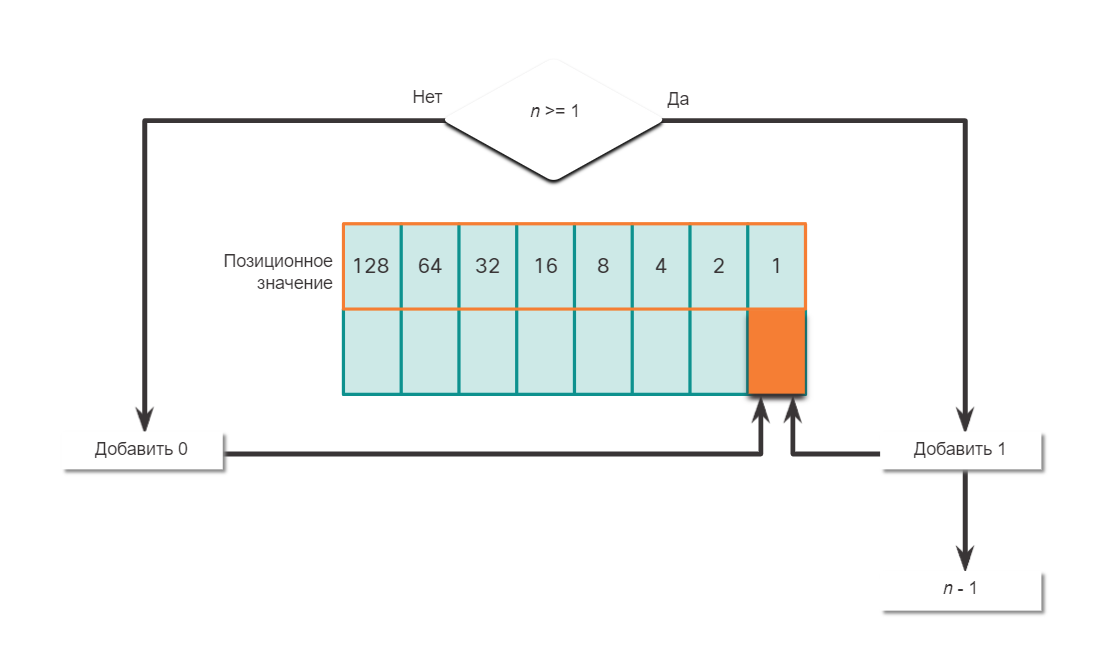
Преобразование десятичных чисел в двоичный формат
Необходимо также понимать, как преобразовывать IPv4-адреса в десятичном формате с точкой-разделителем в двоичный формат. Полезным инструментом является таблица двоичных позиционных значений.
Пример преобразования десятичных чисел в двоичный формат
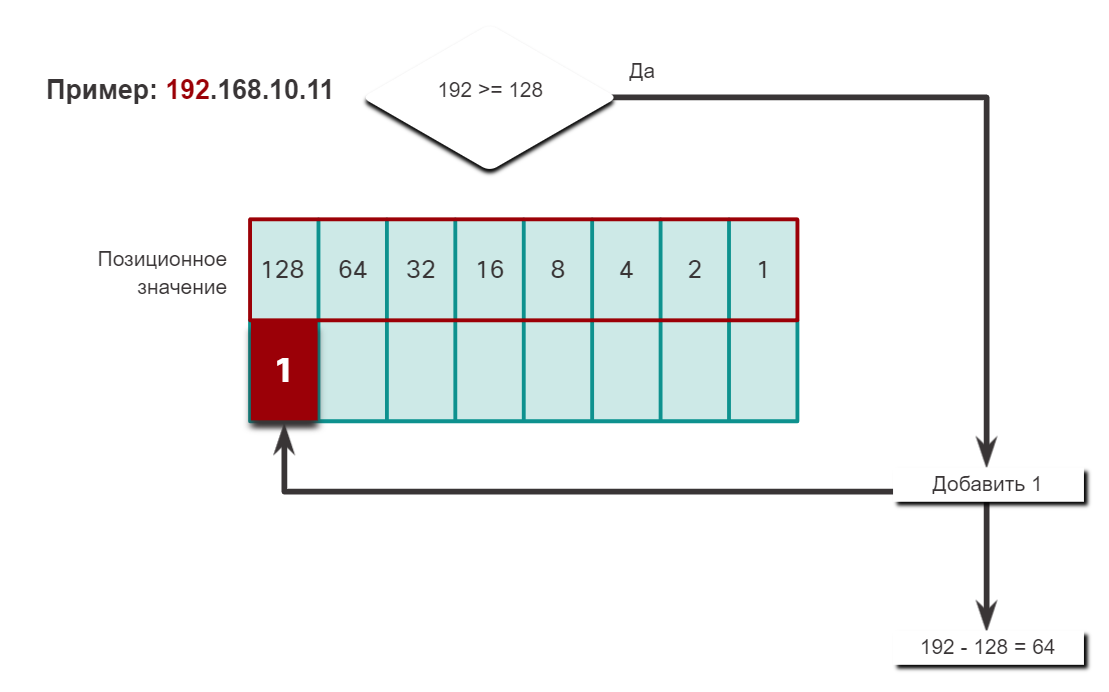
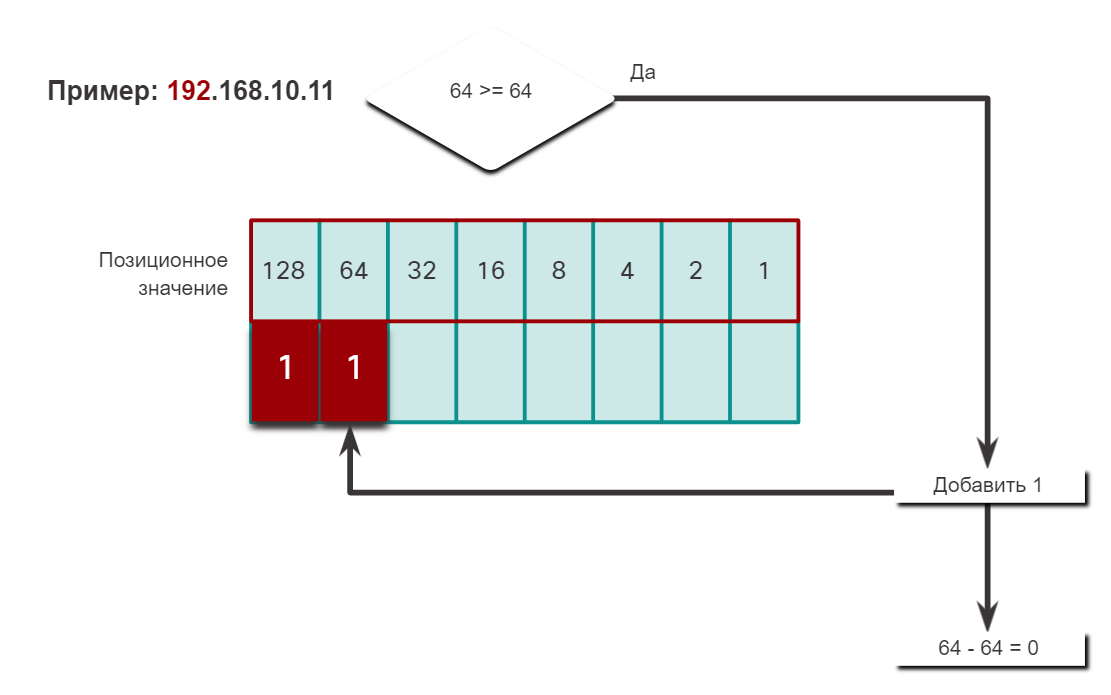
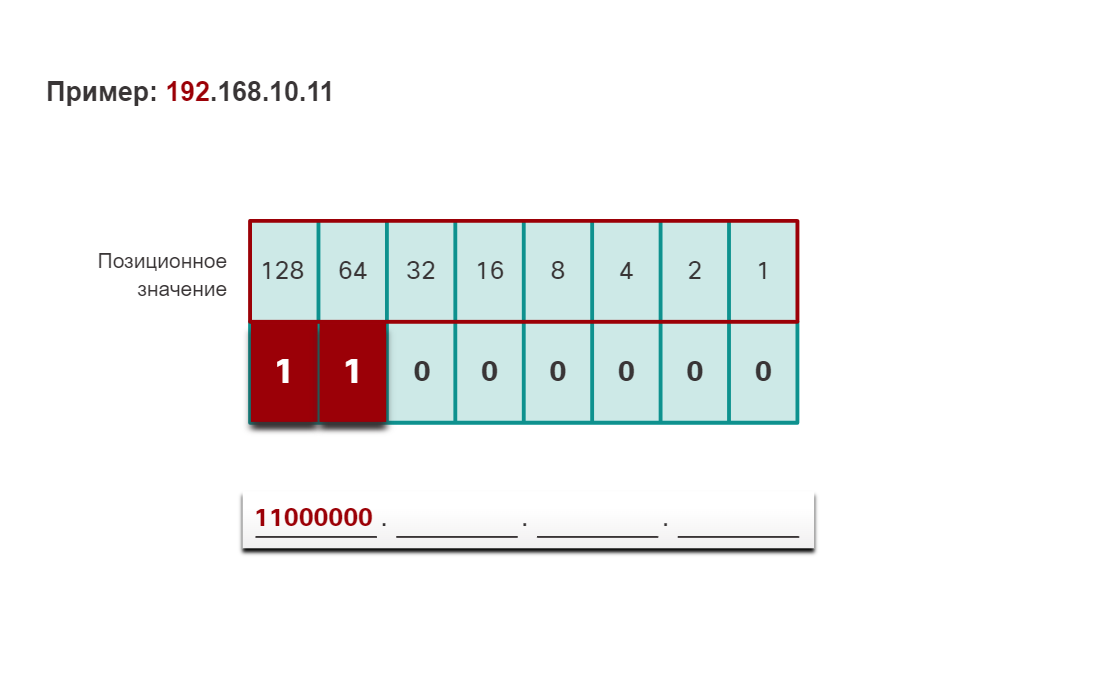
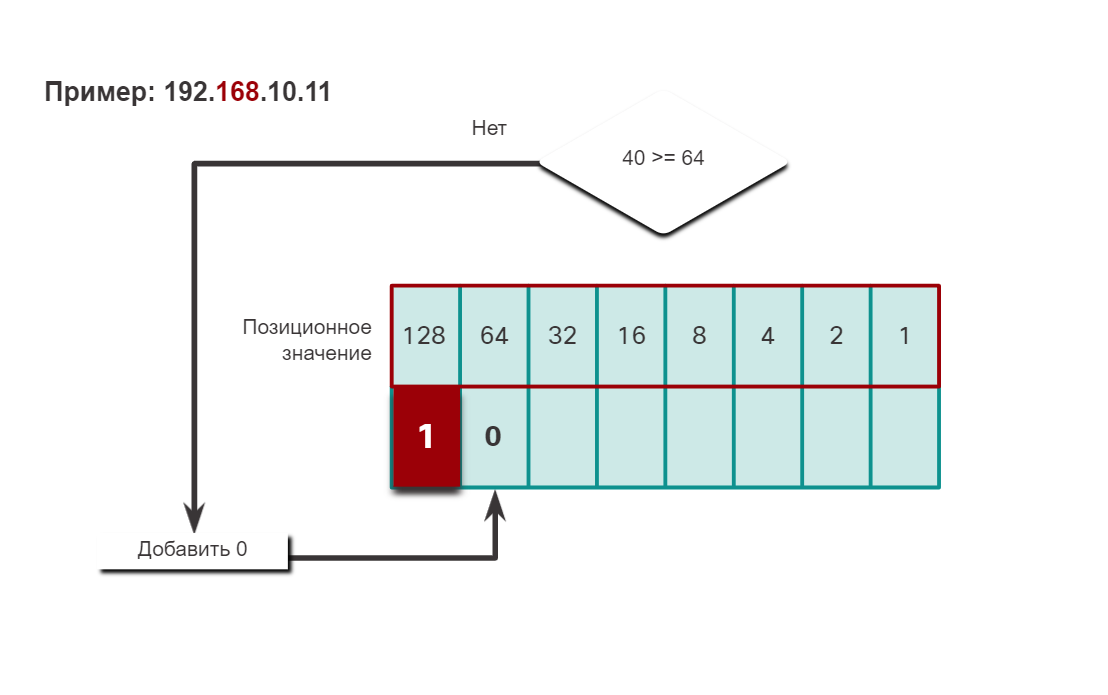
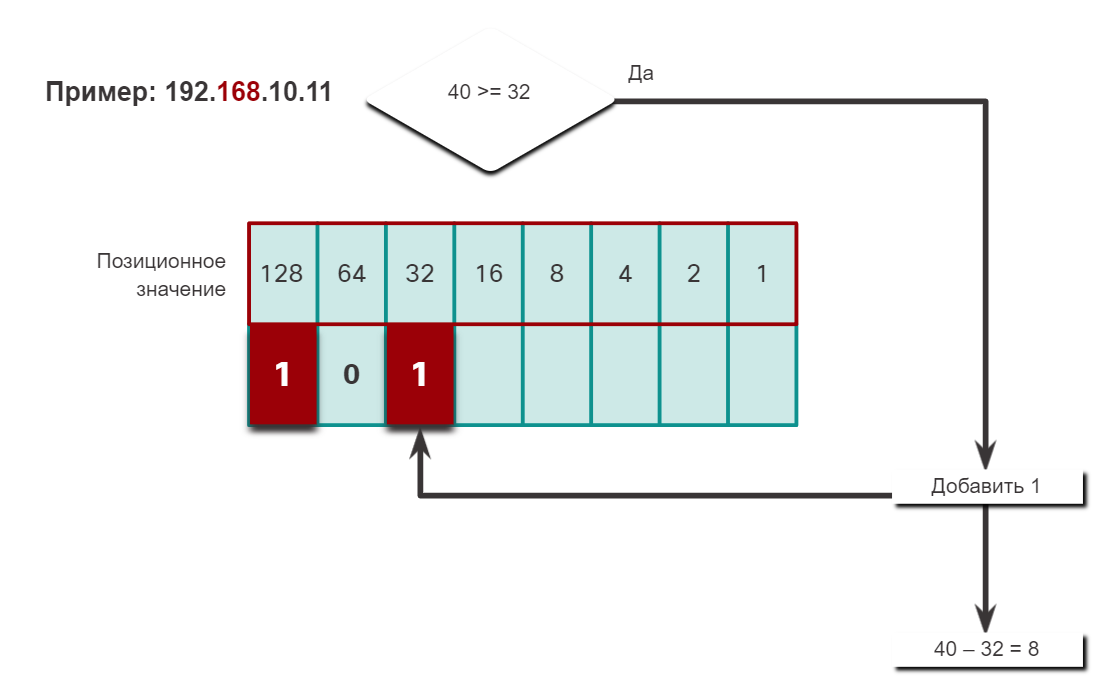
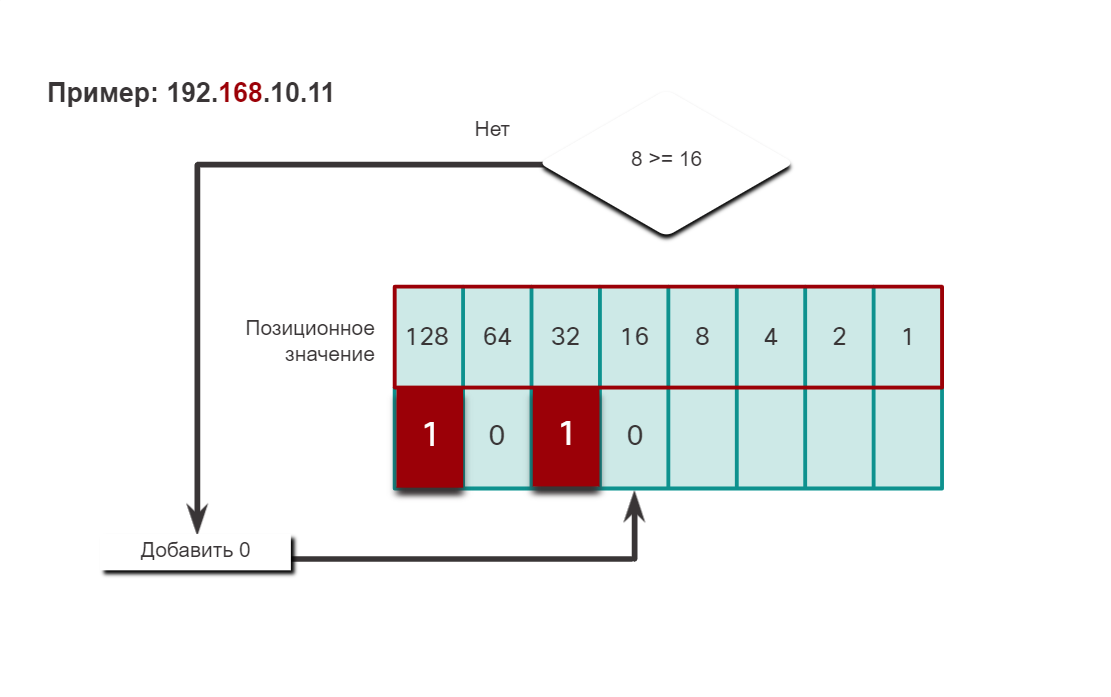
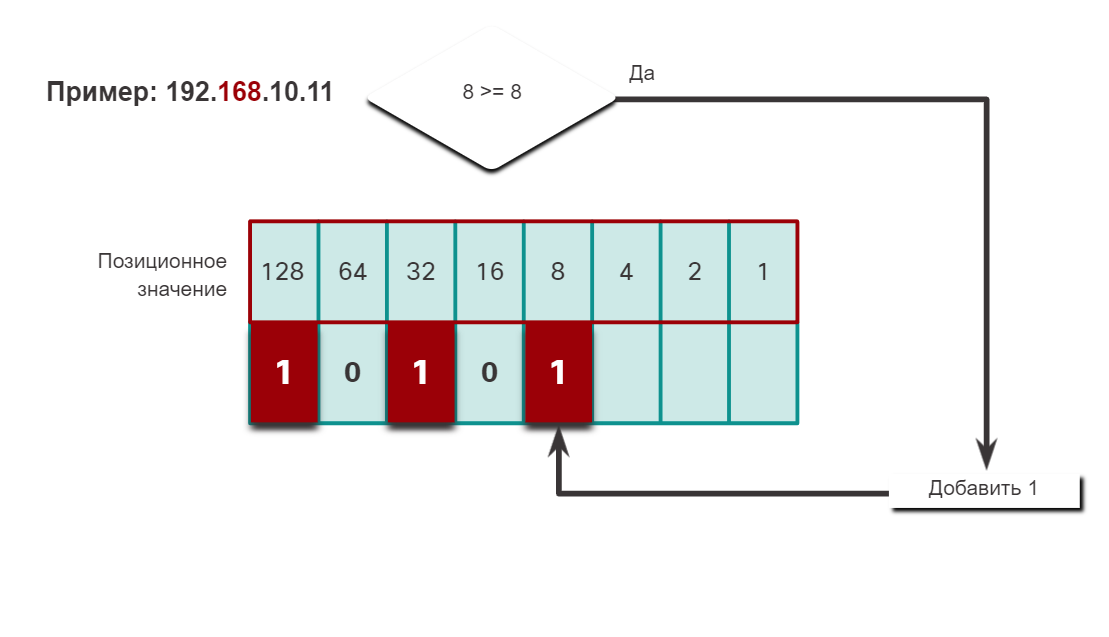
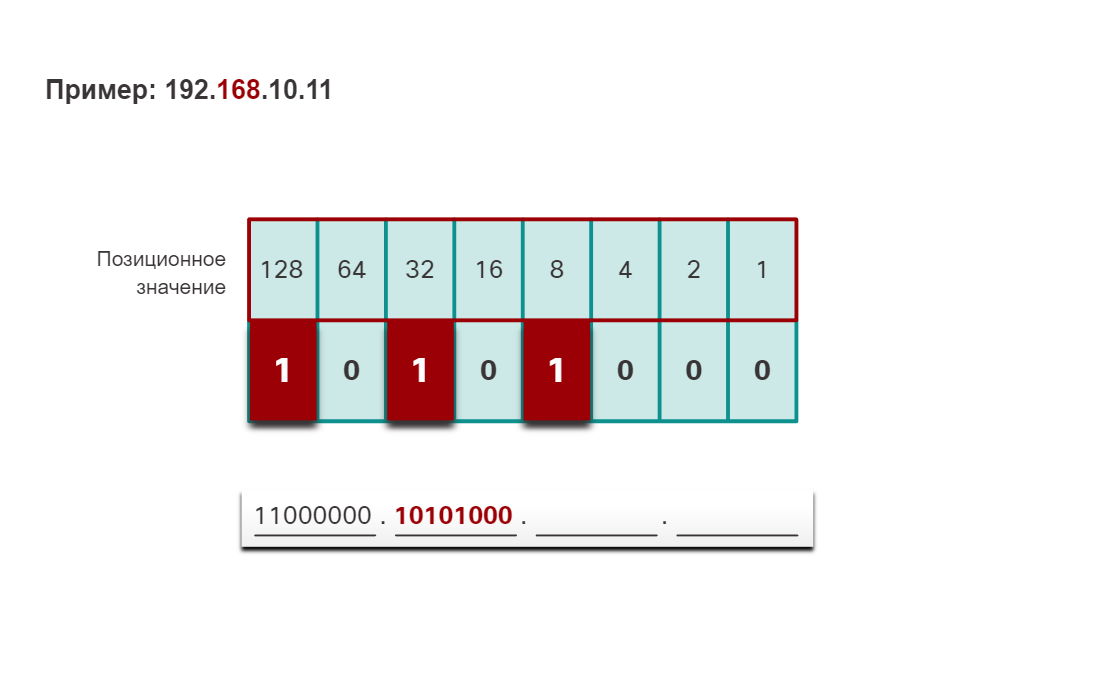
Чтобы лучше понять этот процесс, рассмотрим IP-адрес 192.168.10.11.
Первый октет номер 192 преобразуется в двоичный, используя ранее объясняемый процесс позиционной нотации.
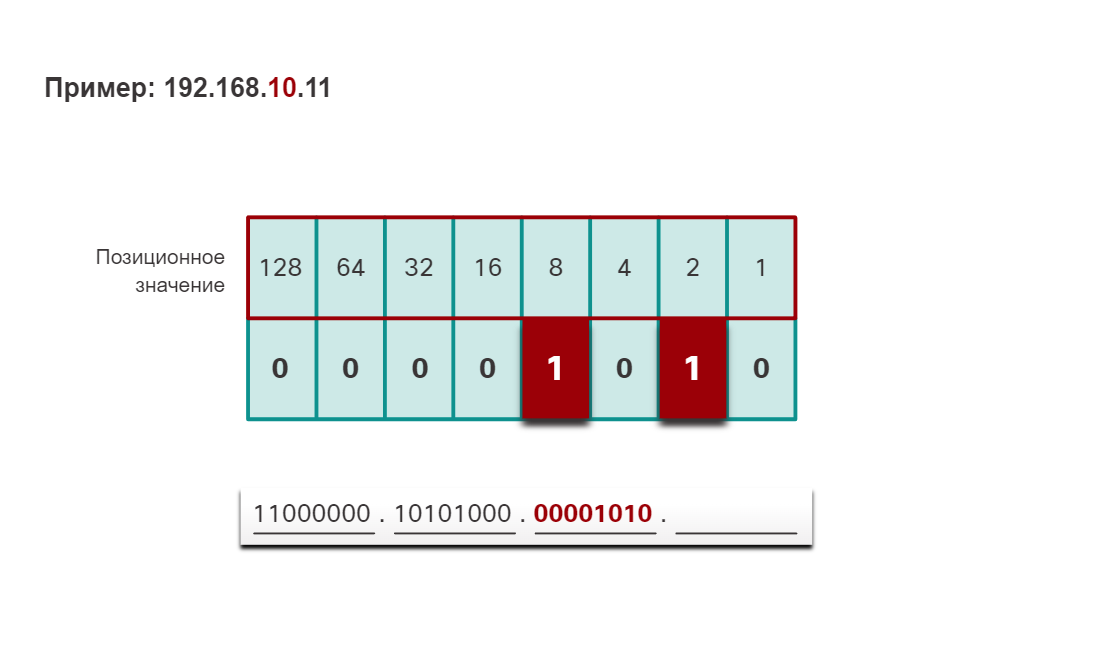
В случае простых или небольших десятичных чисел процедуру вычитания можно пропустить. Это число можно довольно легко получить без вычитания (8 + 2 = 10). Двоичное значение второго октета — 00001010.
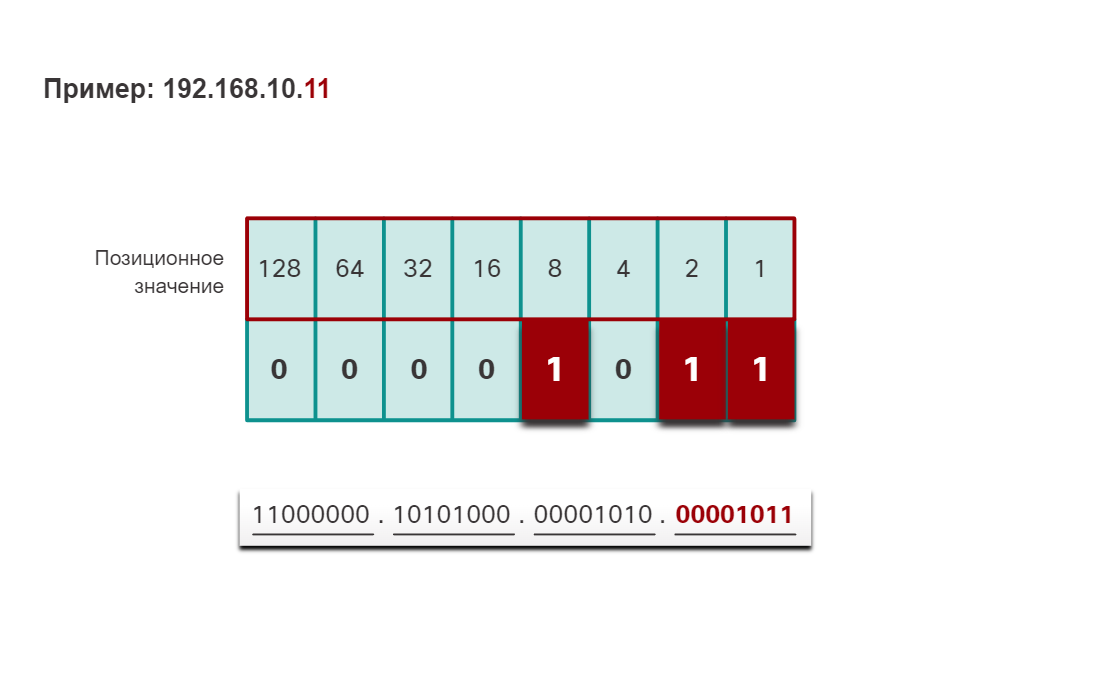
Четвертый октет — 11 (8 + 2 + 1). Двоичное значение второго октета — 00001011.
Преобразование между двоичной и десятичной системами счисления может поначалу показаться сложным, но чем больше вы будете практиковаться, тем проще сможете это делать.
Упражнение - Преобразование десятичных чисел в двоичные
Инструкции
В этом упражнении вы можете на практике отработать преобразование десятичных чисел в 8-битные двоичные значения. Рекомендуется работать с этим инструментом до тех пор, пока вы не сможете выполнить преобразование без ошибок. Преобразуйте десятичное число, показанное в строке «Десятичное значение», в его двоичные биты.
Упражнение. Игра «Двоичные числа»
Это забавный способ узнать бинарные числа для сетей.
Game Link: https://learningnetwork.cisco.com/docs/DOC-1803
Чтобы воспользоваться этой ссылкой, вам нужно войти на сайт cisco.com. Необходимо будет создать учетную запись, если у вас ее еще нет.
Адреса IPv4
Как упоминалось в начале этой темы, маршрутизаторы и компьютеры понимают только двоичные файлы, в то время как люди работают в десятичной системе. Важно, чтобы вы получили полное представление об этих двух системах нумерации и о том, как они используются в сети.